Basic Rocket Propulsion

To induce a propulsion of a system, the system requires thrust; A force exerted to push a system forward. Thrust is achieved by inertia, namely using Newton's First Law of Motion. In Rocketery and in Aircrafts, propulsion given by thrust is dealt in by the engine known as "Working Fluid" and this device uses fluid to expel and create thrust force. In terms of the fluid used, aircraft system usually use air that is sucked in, compressed, heated and then expelled as heavy energenic particles that create thrust to push against the medium and propel the system.

Other Types of Propulsion

Nuclear Thermal Propulsion: Uses a nuclear reactor to expel radiation, as a more efficient but danger mean of propulsion.
Chemicial Propulsion: Uses chemical fluid as an replacement for air.
Eletric Propulsion: Uses ion as particles instead of heated particles.

Types of Rocket

With different type of propulsion comes, the different types of rockets. There are two main types of engine, commonly known as Jet Engines and Rocket Engines.

Jet Engines are a type of engine that carries its own fuel, comprised of oxgyen from the atompshere. This makes them efficient within Earth Atomspheric layer with compressed air as the medium for propulsion but won't work in space.
Rocket Engines on the other hand, carry their own supply of oxygen fuel but require an oxidser that is usually made from liquid oxgyen or compressed air. In rocket engines, a having a fuel and an oxidser makes the concept of propellents. When fuel is combined and burnt, they create thrust!

Solid Rockets

Solid Rockets are a type of rocket engine that combines uses its propellent (fuel and oxidser) with a hole in the middle of the device. Black propellent on the outer cyclinder acts as the igniter to burn the oxygen or create exhausted gas, in the hole. As the exhausted gas flow to the bottom, the nozzle, at the bottom of rocket starts with a tiny dimensional hole, that forced high pressure increasing the force of the compressed particles. This, in turns crate a larger magnitude of thrust.

NOTE: Once a solid rocket is ignited, it is unable to turn off.

Liquid Rockets

Liquid Rockets are a more modern method of rocket propulsion, as unlike solid rockets, can be controlled in terms of how amount fuel and oxidiser is used. Robert Goddard was the first to propose the idea of liquid fuelled rockets. Liquid rockets has their fuel and oxidiser in seperate tanks, which are connected by pipes and are extracted by the used of Turbo Pumps to a combustion chamber with high pressure. With this process, the chamber generates random moving energy in which the nozzle, is implemented to conver the thermal energy to smooth directional kinectic energy. Injector plate (aka Showerheads) are placed at the throat of the rocket each connects the combustion chamber with the nozzle.

Water Rockets

Watter Bottle Rockets are less used, as they are very inefficient and are mainly design for experimental and prototypes. They consist of sourcing water and a bottle as a mean of propulsion.

Newton's Law of Motion

Newton's Laws of Motion are three physical laws that, together, laid the foundation for classical mechanics. They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces.

Newton's 1st Law

states that an object at rest, will remain at rest unless acted upon by an external force, in which inertia propels the object.

Σ F = 0
Σ F = Force(Net) (N)

Newton's 2nd Law

states through the equation, F=ma that acceleration is proportional to its net force and overs its mass.

F = ma
F = Force (N)
m = Mass (kg)
a = Acceleration (m/s^2)

Newton's 3rd Law

states for every action there will be an equal and opposite reaction.

F(Action) = - F(Reaction)
F(Action) = Action Force (N)
- F(Reaction) = Opposite of F(Action) (N)

Ideal Rocket Equation

Initially, t=0
The object is at rest, v=0
Totol Mass: Mass of Payload, Propellent (Fuel and Oxidiser) and Structure (Engine, Frame, Surface)
m(Initial Mass) = m(Payload) + m(Propellent) + m(Structure)

Due to Law of Conversation of Energy, F = ma
where m = m(flow rate) and
v = v(exhaust)
As propollent is used to fuel kinetic energy, it's using up fuel and hence mass
Thus mass is a rate over time (dm/dt)
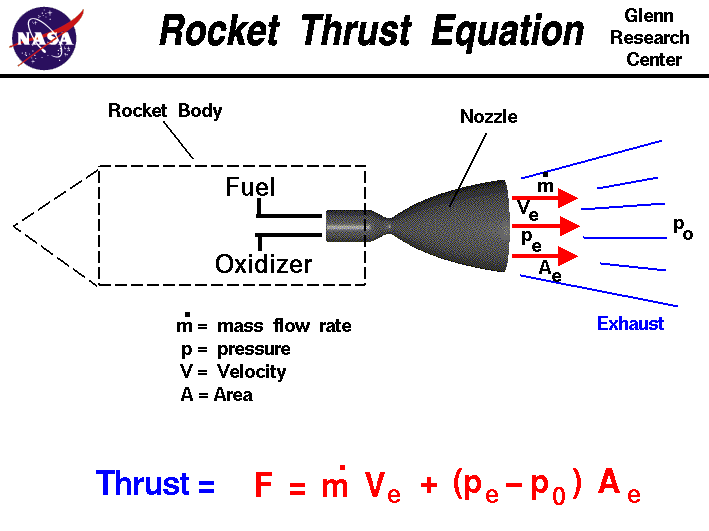
F = m(flow rate) v(exhaust)
F = - (dm/dt) * v(exhaust)
Note: Negative due to rocket travelling in opp. position to the exhaust

At the final stage, propellent is used up
m(final state) = m(initial state) - m(propellent

Again, solving in term of Law of Conservation of Energy

Newton's 2nd = F(rocket) 

        F = m * a , F = - (dm/dt) * v(exhaust) 

        m(a) = - v(exhaust)(dm/dt) 

        m(dv/dt) = - v(exhaust)(dm/dt) 

        Remove dt 

        m(dv) = - v(exhaust)(dm) 

        (dv) = - v(exhaust)(dm/m) 

        Integrate intial to final 

        v(i)∫v(f) (dv) = - v(exhaust) m(i)∫m(f) (dm/m) 

        v(f) - v(i) = - v(exhaust) [ln(m(f)) - ln(m(i))] 

        Remove Negative

Equation

Δv = v(exhaust) [ln(m(i)/m(f))]

Rocket Equation For MultiStage Rockets

For Multistage Rockets consist or two or more propellents, making them heavier and requiring more force than single staged rockets.

Initally t=0
m(intial) = m(payload) + m(structure 1) + m(propellent 1) + m(structure 2) + m(propellent 2)

First Stage As staged of propellent is used up, they are detached.
m(1) = m(payload) + m(structure 1) + m(structure 2) + m(propellent 2)

Second Stage

m(2) = m(payload) + m(structure 2) + m(propellent 2) 

        m(final) = m(payload) + m(structure 2)

Using the Rocket Equation for Multistage Stage:
Δv = v(exhaust) [ln(m(i)/m(f))] Δv = v(exhaust) [ln(m(i1)/m(f1)) + ln(m(i2)/m(f2))] Equation Δv = v(exhaust) [ln(m(i1)m(i2)/m(f1)m(f2))]

Atomspheric Drag in LEO Orbit

For an object to achieve lift off in space, they must have thrust that is greater than their weight
When taking of in a gravity field, astronauts must considers the exhaust veloecity of rocket engines expelling onto the launch pad
as well as, the thrust to weight ratio.

Thrust to weight ratio

If the T-W ration >one then it will lift
If the T-W ration <one then it will not lift

To calculate the force upon liftoff is done by G-Force
That is the Excess Thurst, which is the Total Thrust - Gross Weight
over then Gross Weight

Control System

Actutors, are mechanical machines that allows for the control of movement of a system. In rockets the actutors are Elevons and Tails Rudders, which are used to control movement in the atomspheric flight.

Control Systems

These can involve:

GPS
Gyro
Gompass
Camera

In controls systems, they are often given a design system of a PID Controller
P == Proportional Feedback
I == Integral Feedback
D == Derivative Feedback

PID Controls

In controls systems, they are often given a design system of a PID Controller:
P == Proportional Feedback
I == Integral Feedback
D == Derivative Feedback

Structural Intergrity

To maintain a successful launch, the rocket must have functioning control systems and propulsion systems.
However it also involves maintain its structural integrity in hopes that the rocket is intact when thousands and
throusand of thrust is moving at supersonic speed throughout the system.

Refer to Structural Analysis in Engineering HSC